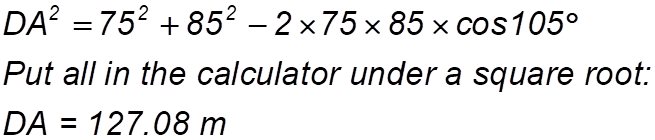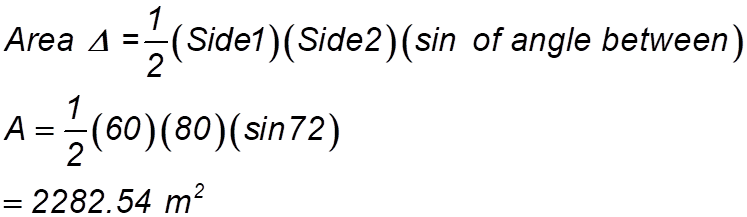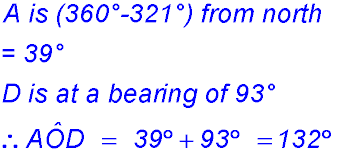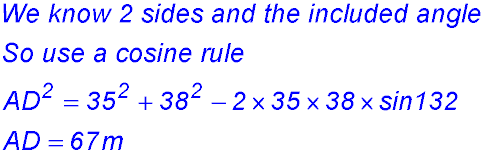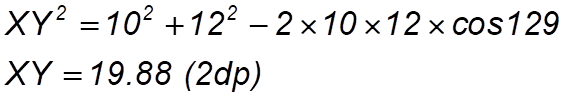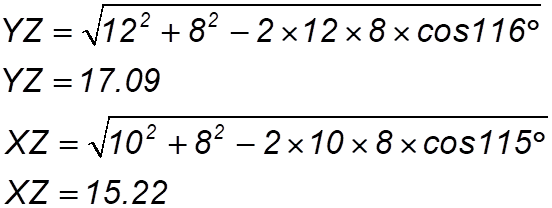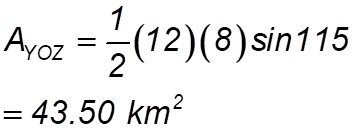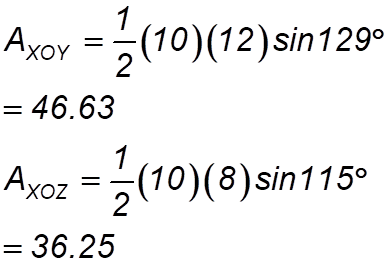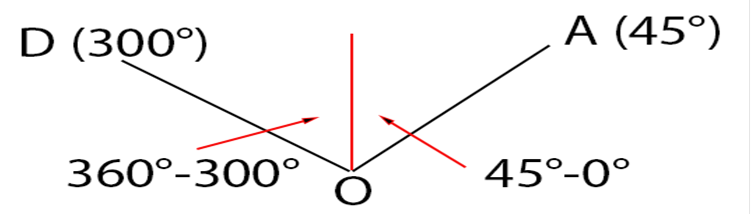
3. (i) Lets draw a vertical from O:

So angle DOA = 60° + 45° = 105°

(ii) Draw another vertical down from O through angle BOC (call it OS(outh):

We now have:
BOS = 180° - 140° = 40°
COS = 212° - 180° = 32°
So BOC = 72°

Then draw two horizontal lines from O – one in each direction (to E and W say) – I like to keep is simple and descriptive – :-)

AOE =90° - 45° = 45°
BOE = 140° - 90° = 50° (or the complement of BOS above)
SO AOB = 45° + 50° = 95°

DOW = 300° - 270° = 30°
COW = 270° - 212° = 58°
SO COD = 88°

Add these 4 angles together to check. AAhh – 360° as we want.

(iii)  For the distance DA we are looking at the triangle at the top. What do we know about that triangle?
Well we know the length of OD and OA and we know the angle between these two sides.
Two sides, One angle and we need the third side:
COSINE RULE.

(iv)

4.

(i)

(ii)

(iii)

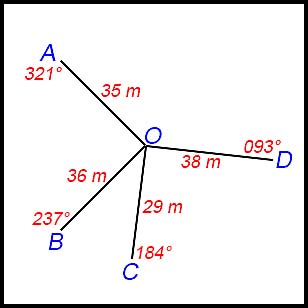
We do the same sorts of things:

(i) Draw in the vertical to N:
XOY = XON + NOY
= (360°-315° = 45°)  + (84°) = 129°

ZOY = ZOS + SOY
= (200°-180° = 20°) +(180°-84° = 96°) = 116°

XOZ = XOW + WOZ
= (315°-270°= 45°) + (270° – 200° = 70°) =115°

Quick check to see if they add up: 129° + 116° + 115° = 360°
They DO ADD UP – what a relief.

(ii) So many questions in maths are of the same type. So get used to picking the strategy to use in given situations.
In triangle XYO, we know two sides (XO and YO) and the angle between those two lines (129°). So again we know 2 sides one angle and need to find the third side – so again COS RULE:

Use 2 dp unless your are told otherwise.
Remember all that calculation went into the calculator in one go (under the root sign).

(iii) Do the same calculation twice more – yes boring (but you get marks:



(iv)


(v) Repeat that calculation twice more (Boring but marks and you still have the format in your calculator:

(vi) So total area = 36.25 + 46.63+43.50 = 126.38 km2